A la fin des années 70, Jean Morlet, alors ingénieur Elf Aquitaine, isole empiriquement une nouvelle classe de fonctions, fruit de l'analyse des signaux réfléchis par le sous-sol, décomposés en éléments simples ayant tous la même forme quelle que soit l'échelle : les ondelettes.

Mais la compagnie ne croit pas à cette nouvelle façon de collecter et d'interpréter les données sismique "si ça marchait ; ça se saurait". Une telle sentence sonnerait la fin de toute science, si des scientifiques curieux tel Yves Meyer, trompant l'attente devant la photocopieuse de l'Ecole polytechnique un jour de 1984, ne jetaient un oeil par dessus l'épaule du collègue en train de photocopier devant lui un article de Morlet et Grossmann, alors à Marseille, qui lui rappelle une théorie mathématique qu'il connait bien (les opérateurs de type Calderon).

Yves Meyer saute ainsi dans le premier train pour vérifier l'un de ces liens inconnus et inexploités, aux conséquences inattendues qui ont marqué l'histoire des mathématiques. Il va ainsi démontrer, généraliser, et étendre la pertinence des décompositions en ondelettes qui, de simples outils d'analyse de signaux géophysiques utilisés pour la détection pétrolière, vont permettre des échanges fructueux entre de nombreuses communautés scientifiques qui s'ignoraient, et des applications remarquables en traitement d'images et du signal, jusqu'à la récente détection des ondes gravitationnelles.

Les décompositions multi-échelles étaient déjà familières aux spécialistes de traitement du signal et de l'image (c'est l'idée d'une image observée simultanément à plusieurs résolutions) mais la formalisation mathématique qu'en donnent les bases d'ondelettes leur confère une puissance incomparable.

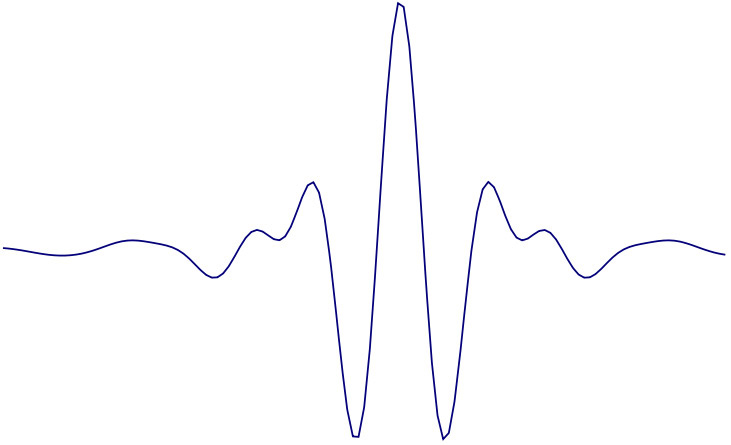Une base d'ondelettes a une structure algorithmique particulièrement simple : ses éléments ont tous la même forme, et se déduisent les uns des autres par translation et dilatation. Certaines bases d'ondelettes existaient déjà (la première est celle d'Alfréd Haar en 1909), mais elles étaient composées de fonctions constantes par morceaux ; la construction de telles bases avec des fonctions régulières semblait même impossible.

Grâce à Yves Meyer, les ondelettes sont devenues un outil universel (adapté à n'importe quel cadre fonctionnel, et fournissant dans chaque cas une décomposition numériquement stable - on dit que ce sont des "bases inconditionnelles") et un outil incontournable en traitement  d'images.

Les "paquets d'ondelettes" puis les "bases trigonométriques locales" de Meyer et Coifman sont des familles de bases qui ont ouvert la voie au domaine porteur des "dictionnaires" de fonctions : ensembles extrêmement redondants, au sein desquels on cherche une sous-famille composée d'un très petit nombre d'éléments, qui permet de représenter le signal très économiquement, et avec une très haute précision.

Parmi les proches collaborateurs qui, à ses côtés, feront le succès des ondelettes, on retrouve : Ronald Coifman ; Stéphane Mallat, qui introduira les algorithmes de  décomposition rapide pour effectuer le traitement des signaux et des images en temps réel ; Ingrid Daubechies, qui construira les premières ondelettes à support  compact ; ou David Donoho, qui développera le potentiel des méthodes d'ondelettes en statistique...